Мы хотим сделать этот проект с открытым исходным кодом доступным для людей во всем мире. Пожалуйста, помогите нам перевести это руководство на другие языки.
КупитьEPUB/PDF
Карта учебника
7 июня 2022 г.

Кривые Безье

Материал на этой странице устарел, поэтому скрыт из оглавления сайта.

Более новая информация по этой теме находится на странице https://learn.javascript.ru/bezier-curve.

Кривые Безье используются в компьютерной графике для рисования плавных изгибов, в CSS-анимации и много где ещё.

Несмотря на «умное» название – это очень простая штука.

В принципе, можно создавать анимацию и без знания кривых Безье, но стоит один раз изучить эту тему хотя бы для того, чтобы в дальнейшем с комфортом пользоваться этим замечательным инструментом. Тем более что в мире векторной графики и продвинутых анимаций без них никак.

Виды кривых Безье

Кривая Безье задаётся опорными точками.

Их может быть две, три, четыре или больше. Например:

По двум точкам:

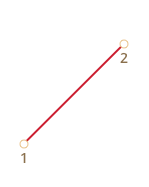
По трём точкам:

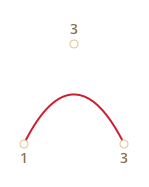
По четырём точкам:

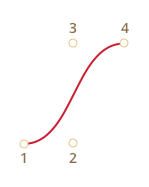
Если вы посмотрите внимательно на эти кривые, то «на глазок» заметите:

  1. Точки не всегда на кривой. Это совершенно нормально, как именно строится кривая мы рассмотрим чуть позже.

  2. Степень кривой равна числу точек минус один. Для двух точек – это линейная кривая (т.е. прямая), для трёх точек – квадратическая кривая (парабола), для четырёх – кубическая.

  3. Кривая всегда находится внутри выпуклой оболочки, образованной опорными точками:

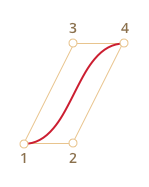
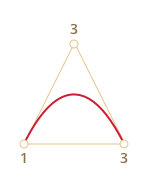
    Благодаря последнему свойству в компьютерной графике можно оптимизировать проверку пересечений двух кривых. Если их выпуклые оболочки не пересекаются, то и кривые тоже не пересекутся.

Основная ценность кривых Безье для рисования – в том, что, двигая точки, кривую можно менять, причём кривая при этом меняется интуитивно понятным образом.

Попробуйте двигать точки мышью в примере ниже:

Как можно заметить, кривая натянута по касательным 1 → 2 и 3 → 4.

После небольшой практики становится понятно, как расположить точки, чтобы получить нужную форму. А, соединяя несколько кривых, можно получить практически что угодно.

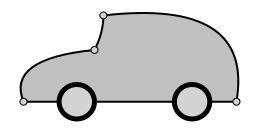
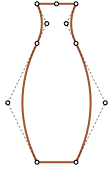
Вот некоторые примеры:

Математика

У кривых Безье есть математическая формула.

Как мы увидим далее, для пользования кривыми Безье знать её нет особенной необходимости, но для полноты картины – вот она.

Координаты кривой описываются в зависимости от параметра t⋲[0,1]

  • Для двух точек:

    P = (1-t)P1 + tP2

  • Для трёх точек:

    P = (1−t)2P1 + 2(1−t)tP2 + t2P3

  • Для четырёх точек:

    P = (1−t)3P1 + 3(1−t)2tP2 +3(1−t)t2P3 + t3P4

Вместо Pi нужно подставить координаты i-й опорной точки (xi, yi).

Эти уравнения векторные, то есть для каждой из координат:

  • x = (1−t)2x1 + 2(1−t)tx2 + t2x3
  • y = (1−t)2y1 + 2(1−t)ty2 + t2y3

Вместо x1, y1, x2, y2, x3, y3 подставляются координаты трёх опорных точек, и в то время как t пробегает множество от 0 до 1, соответствующие значения (x, y) как раз и образуют кривую.

Впрочем, это чересчур наукообразно, не очень понятно, почему кривые именно такие, и как зависят от опорных точек. С этим нам поможет разобраться другой, более наглядный алгоритм.

Рисование «де Кастельжо»

Метод де Кастельжо идентичен математическому определению кривой и наглядно показывает, как она строится.

Посмотрим его на примере трёх точек (точки можно двигать). Нажатие на кнопку «play» запустит демонстрацию.

Алгоритм построения кривой по «методу де Кастельжо»:

  1. Рисуем опорные точки. В примере выше это 1, 2, 3.

  2. Строятся отрезки между опорными точками 1 → 2 → 3. На рисунке выше они коричневые.

  3. Параметр t пробегает значения от 0 до 1. В примере выше использован шаг 0.05, т.е. в цикле 0, 0.05, 0.1, 0.15, ... 0.95, 1.

    Для каждого из этих значений t:

    • На каждом из коричневых отрезков берётся точка, находящаяся от начала на расстоянии от 0 до t пропорционально длине. Так как коричневых отрезков – два, то и точек две штуки.

      Например, при t=0 – точки будут в начале, при t=0.25 – на расстоянии в 25% от начала отрезка, при t=0.5 – 50%(на середине), при t=1 – в конце отрезков.

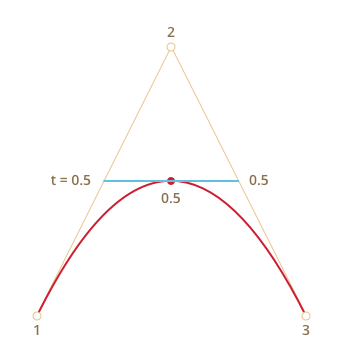
    • Эти точки соединяются. На рисунке ниже соединяющий их отрезок изображён синим.

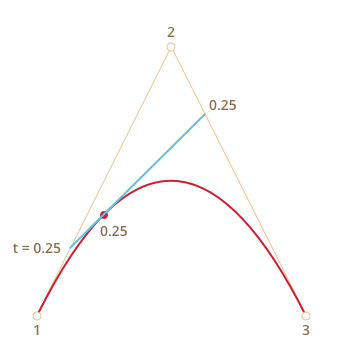
При t=0.25 При t=0.5

  1. На получившемся отрезке берётся точка на расстоянии, соответствующем t. То есть, для t=0.25 (первый рисунок) получаем точку в конце первой четверти отрезка, для t=0.5 (второй рисунок) – в середине отрезка. На рисунках выше эта точка отмечена красным.

  2. По мере того как t пробегает последовательность от 0 до 1, каждое значение t добавляет к красной кривой точку. Совокупность таких точек для всех значений t образуют кривую Безье.

Это был процесс для построения по трём точкам. Но то же самое происходит и с четырьмя точками.

Демо для четырёх точек (точки можно двигать):

Алгоритм:

  • Точки по порядку соединяются отрезками: 1 → 2, 2 → 3, 3 → 4. Получается три коричневых отрезка.
  • На отрезках берутся точки, соответствующие текущему t, соединяются. Получается два зелёных отрезка.
  • На этих отрезках берутся точки, соответствующие текущему t, соединяются. Получается один синий отрезок.
  • На синем отрезке берётся точка, соответствующая текущему t. При запуске примера выше она красная.
  • Эти точки описывают кривую.

Этот алгоритм рекурсивен. Для каждого t из интервала от 0 до 1 по этому правилу, соединяя точки на соответствующем расстоянии, из 4 отрезков делается 3, затем из 3 так же делается 2, затем из 2 отрезков – точка, описывающая кривую для данного значения t.

Нажмите на кнопку «play» в примере выше, чтобы увидеть это в действии.

Ещё примеры кривых:

С другими точками:

Петелька:

Пример негладкой кривой Безье:

Так как алгоритм рекурсивен, то аналогичным образом могут быть построены кривые Безье и более высокого порядка: по пяти точкам, шести и так далее. Однако на практике они менее полезны. Обычно используются 2-3 точки, а для сложных линий несколько кривых соединяются. Это гораздо проще с точки зрения поддержки и расчётов.

Как провести кривую Безье через нужные точки?

В задаче построения кривой Безье используются «опорные точки». Они, как можно видеть из примеров выше, не лежат на кривой. Точнее говоря, только первая и последняя лежат на кривой, а промежуточные – нет.

Иногда возникает другая задача: провести кривую именно через нужные точки, чтобы все они лежали на некой плавной кривой, удовлетворяющей определённым требованиям. Такая задача называется интерполяцией, и здесь мы её не рассматриваем.

Существуют математические формулы для таких построений, например многочлен Лагранжа.

Как правило, в компьютерной графике для построения плавных кривых, проходящих через несколько точек, используют кубические кривые, плавно переходящие одна в другую. Это называется интерполяция сплайнами.

Итого

Кривые Безье задаются опорными точками.

Мы рассмотрели два определения кривых:

  1. Через математическую формулу.
  2. Через процесс построения де Кастельжо.

Их удобство в том, что:

  • Можно легко нарисовать плавные линии вручную, передвигая точки мышкой.
  • Более сложные изгибы и линии можно составить, если соединить несколько кривых Безье.

Применение:

  • В компьютерной графике, моделировании, в графических редакторах. Шрифты описываются с помощью кривых Безье.
  • В веб-разработке – для графики на Canvas или в формате SVG. Кстати, все живые примеры выше написаны на SVG. Фактически, это один SVG-документ, к которому точки передаются параметрами. Вы можете открыть его в отдельном окне и посмотреть исходник: demo.svg.
  • В CSS-анимации, для задания траектории или скорости передвижения.
Карта учебника